Major Scales and Keys

In music, a scale is a group of "allowed" notes in a certain key. For example, in the key of C major, the allowed notes are C, D, E, F, G, A, B, and, again, the next higher C. The notes of C# (C sharp), Eb (E flat), F#, Ab, and Bb are not officially allowed. 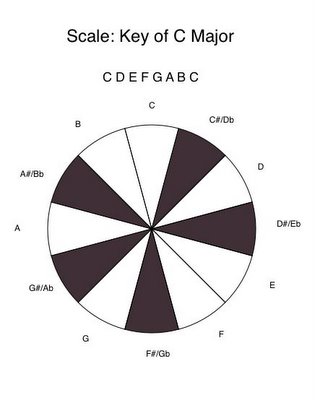The notes that aren't allowed in C major are the black keys on a piano. You can play a C major tune without ever touching a black key.

(Each black key has two names, by the way. For example, the F# key is also the Gb key. F# and Gb are said to be enharmonics of one another: they're the same note called by two different names.)

Notice in the diagram that the disallowed notes in black are not evenly distributed around the circle of the octave. Nor is the octave circle symmetrical. It would possess a form of symmetry if, for instance, you made the F note black, or if you made the F#/Gb note white. But there is no way to distribute five black, disallowed notes and seven white, allowed notes around an octave circle of 12 notes and have the result be either evenly distributed or symmetrical.

You can mentally rotate this C major octave circle, along with the associated note names, to any of 11 different positions other than the one shown. For example, you can imagine moving, say, the note of E to the top of the circle, such that E tries to be the so-called tonic or root note of a major scale.

But if you do it that way, the pattern of black, disallowed notes does not match up with the original pattern. In the original pattern, the "next" note after the "top" note of C, which is C# (moving clockwise), is black. But now, the "next" note after the "top" note of E, which is F, isn't black. It's white. So the pattern of black, disallowed notes doesn't match the original pattern.

In fact, no note which you might wish to put on top, other than C, gives exactly the same major scale pattern, which is, clockwise from the "top":

white-black-white-black-white-white-black-white-black-white-black-white

The only way to get the same pattern in a different major key is to rotate the note names as a group, but not the circle itself. Leave the pattern-giving circle alone.

Here's what I mean. Say you want F on top as the tonic note of the (you guessed it) F major scale. Just rotate the note names, all by themselves as a group, seven positions clockwise: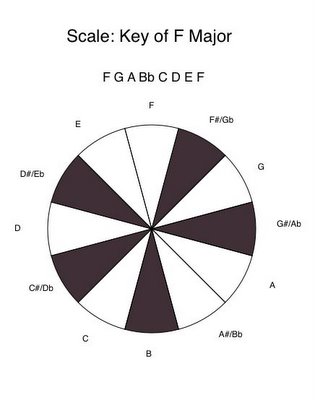Notice now that one of the piano's white keys, B, is no longer allowed, as it was in the key of C major. Instead, the black key known as Bb (or A#) is included in the F major scale. Notice, accordingly, that the black-white pattern of the octave circle is not necessarily that of the piano keys used for a given major key. In fact, C major is the only major key for which the black segments of the octive circle exactly match the black keys of the piano keyboard. (True, there is one minor key, A minor, that exactly matches the keyboard and thus uses only white keys ... but I'm not discussing minor keys here, only major ones.)

Of course, there's no law against including an unflatted B note in a tune written in the key of F major — but to do it in music notation, you have to put a natural sign before the note. Then, in playing the tune on a piano, you strike the B key (white) instead of the Bb key (black).

Rotating the note names as a group, while leaving the octave circle alone, you can in this way come up with twelve different major keys. The set of allowed notes in each are different, and unique. Here's Db major: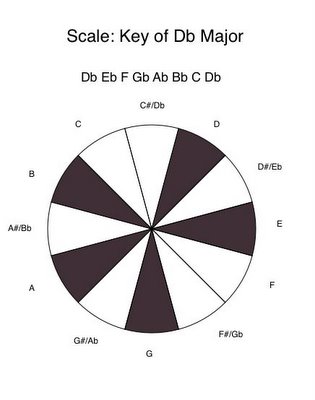Now five of the notes in the C major scale have been flatted: D, E, G, A, and B have become Db, Eb, Gb, Ab, and Bb.

So the actual notes which are "allowed" in a given major scale differ from one scale to the next. Yet the black-white pattern remains the same.

This distinctive black-white pattern is picked up by the ear after only a few notes are played, allowing the ear to "figure out," unconsciously of course:

• that the scale is indeed a major scale — not, say, a minor scale, for which the black-white pattern of the octave circle is different
• that the scale's root note or tonic is ... whichever note it happens to be (C in the first example, F in the second, Db in the third)
• which other notes are "allowed" in this major scale, and therefore which notes are not allowed
  

The scale's root note or tonic determines which of the twelve possible major keys this key is. That is the note to which the ear expects the melody to return to and finish on. And most simple melodies and many complex ones do indeed contrive to wind up on the tonic note of the scale the melody is built from.

The "allowed" notes in the scale are also typically the "allowed" notes in the chords to which the melody is customarily set. For example, when a measure of a C major melody features the notes of C and E, often the associated chord played on a guitar or piano will be the C major triad of C-E-G. If G and B are being emphasized in the measure in question, possibly the associated chord will be the G major triad, G-B-D.

Accordingly, the G minor triad of G-Bb-D will usually not be heard in the harmony accompaniment for a C major melody. Why? Because Bb is not one of the "allowed" notes in the C major scale.

By the same token, G-Bb-D will crop up in melodies written in the key of F major, while the G-B-D triad is considered odd. Why? Because Bb is a part of the F major scale, while unflatted B is not.

Thus, an awful lot of wisdom about keys, scales, and associated chords derives from the simple fact that the disallowed (in the octave-circle diagrams, black) notes of a major key — and this is true, in a like way, also of a minor key — are not evenly or symmetrically distributed around the octave circle.

More on Pandora

Here's an East Bay Express article about Pandora, the Internet radio site I covered in Viva Pandora!. I'm still grooving on the sheer abundance of good music it will serve up to you, if you tell it a favorite artist or song title. I now have 34 songs stacked up in my Apple Music Store shopping cart, and I'm not even trying real hard to snag every hot lick and tuneful tour de force I hear.

Pandora ranks the over 300,000 songs in its library according to hundreds of musical "genes" identified by the Music Genome Project as constituting the best way to analyze song tracks for perhaps surprising similarities. For example, according to the article, "whether the kick drum sound is tight or booming" is one of 235 genes identified for the hip-hop/electronic genre. However, the jazz genre's "gene that counts improvised sax licks" is, obviously, not, though it is one of the total of 400 or so genes spread across those two genres and also those of rock/pop/country and world music.

I find it fascinating — and here's something you won't glean from the Pandora FAQ — that Pandora constructs a stream made up of tight, mood-similar sets. It

... builds a series of short playlists around common elements, much the way a real-life deejay puts music together into sets, first establishing one mood, then breaking it for another one ... [T]he site plays a set tightly connected to the original request in some way, then moves on to another set that's related a different way.

If I had my way, I'd ask that Pandora provide a way to quickly skip ahead not only to the next song but to the next set ... i.e., to take me to the next mood.

Music Theory Explained ... Quite Well!

Ever wonder exactly how music works? How songs can burrow their way into our souls and remain there for a lifetime? Are there things great pieces of music have in common?

Actually, nearly all popular music has certain things in common ... melodies written in a definite key, chord progressions that go with and enhance the melody, rhythms and tempos carefully calculated to set up an infectious groove, accessible melodic hooks and insistent instrumental riffs that stick in the head, and so on.

The Complete Idiot's Guide to Music Theory by Michael Miller explains all the theoretical stuff underlying all the wonderful music in the world — and also most of the not-so-great music, of course — and explains it quite well!

I've read any number of books that focus on music theory, or that contain chapters on theory within a larger context such as learning to play guitar. All the others fail, in my humble opinion, to actually teach theory. They tell you — sometimes well, sometimes poorly — rather than teach you.

The difference is that, as you read the Miller book, you grok the theory ... you don't just know it, shallow as human knowledge can sometimes be — and can remain, if it's not all too quickly forgotten.

Miller is an excellent educator, and somehow he manages to feed you all the things you need, in just the right order, without overwhelming you at any point with information that makes no sense or that is simply too much, too soon.

Viva Pandora!

Ever wished for an Internet radio station that you can really tailor to your tastes? Now there's Pandora, and you can.

The Pandora player you see the first time you visit (the snap at right is from much later in my Pandora noodling career) asks you to name an artist or song you really like. I entered "Paul McCartney." The player responded by playing a song by Sir Paul (the recent Chaos and Creation in the Back Yard track "Riding to Vanity Fair"), and then began choosing other songs that, though they may typically be by other artists, have key characteristics in common (mixed acoustic and electric instrumentation, subtle use of vocal harmony, major key tonality, and prominent percussion, for instance) with songs by Macca himself.

The second song in the Pandora-generated series, "Wherever You Are" by David Mead, was by an artist I'd never heard of, but one who (at least in that song) sounded almost like a Paul clone. I liked the sound, so I gave it a thumbs up in the Pandora player. That meant Pandora would henceforth bias my "Paul McCartney Radio" playlist toward Macca-like music that was also David Mead-like.

In fact, I liked "Wherever You Are" so much, I told the Pandora player to link to it ("buy" it, supposedly) in Apple's iTunes Music Store. This kind of activity causes the iTunes app to launch if it isn't already active, while Pandora continues to play. The appropriate search criteria are automatically passed from Pandora to the Music Store search engine, and the song you want (in possibly more than one version by the artist in question) appears in the iTunes results window. From there, I could click on "buy song" mext to one of these versions to have the song I'd told Pandora I liked and wanted put in my shopping cart, ready to purchase.

But, maddeningly, the Apple Store's music library is missing some key artists almost entirely — including McCartney, and also including the Beatles and Wings. If I try to buy a missing song, iTunes simply says "Your search did not return any results" and folds its hands complacently.

Actually, I ran into some additional snags the first time I tried to "buy" a song at iTunes courtesy of Pandora, and I had to resort to some clever computer-type strategies to get things working smoothly thenceforth. But the fact that this pass-off works at all (or can fairly easily be made to work) is a bit amazing.

But not as amazing as the fact that Pandora really does know how to pick music that matches, in this instance, my taste for Paul McCartney. Or, on another "station" I set up, this one for "Outlaw Country" stars Willie Nelson, Johnny Cash, Waylon Jennings, and Kris Kristofferson — the "Highwaymen" — plus, of course, their country cousin Merle Haggard. If I wanted, I could add Jerry Jeff Walker, and his "musical genome" would influence any subsequent selections Pandora makes on that particular station.

Yes, "musical genome" is the apt phrase — not "musical genre." What is a musical genome? Well, it's something defined by the Music Genome Project under the aegis of Tim Westergren, who is also Pandora's prime mover. According to this story in my local newspaper, the project broke popular music down into 400 parameters (one is, for instance, "use of vocal harmony") which could be used to describe any given song in the repertoire.

Every song in Pandora's 300,000-song library has been rated according to all 400 parameters by music theory-trained analysts whose correct judgments are absolutely crucial to the Pandora/Music Genome concept. As far as I can tell, the analysts are spot-on every time.

So far, I'm approximately six hours into my new Pandora lifestyle, and I've created five custom-tailored stations and found 19 songs to put in my Apple Music Store shopping cart. A few of the songs are ones I've heard before but never thought to buy. Most of them are brand new to me. Many or them are by artists I've never followed ... including four artists I've not heard of before!

So, yes, finally there's a way of setting up Internet radio stations to play music you're actually gonna like, even if it's brand new to you. Check it out!

P.S. By the way, Pandora is free! Supposedly, you have to look at ads ... but for whatever reason, I've yet to see an ad. If you want to make sure you never see an ad, you can pay Pandora $36 a year of use, or $12 for a shorter, three-month subscription.